กฎการเคลื่อนที่ข้อที่ 3
ตามกฎการเคลื่อนที่ข้อที่ 1 และ 2 ของนิวตันเป็นการอธิบายความสัมพันธ์ระหว่างแรงกับการเปลี่ยนสภาพการเคลื่อนที่ของวัตถุ เมื่อแรงภายนอกมากระทำต่อวัตถุ นอกจากนี้นิวตันยังพบว่าในขณะที่มีแรงกระทำต่อวัตถุ วัตถุจะออกแรงโต้ตอบต่อแรงที่มากระทำนั้นโดยทันทีทันใด เช่น ถ้าเรายืนบนสเก็ตบอร์ดหันหน้าเข้าหาผนังแล้วออกแรงผลักฝาผนัง เราจะเคลื่อนที่ออกจากฝาผนัง การที่เราสามารถเคลื่อนที่ได้แสดงว่าจะต้องมีแรงจากฝาผนังกระทำต่อเรา ถ้าเราผลักฝาผนังด้วยขนาดแรงมากขึ้น แรงที่ฝาผนังกระทำกับเราก็มากขึ้นตามไปด้วย โดยเราจะเคลื่อนที่ออกห่างจากผนังเร็วขึ้น หรือเมื่อเราออกแรงดึงเครื่องชั่งสปริง เราจะมีความรู้สึกว่าเครื่องชั่งสปริงก็ดึงมือเราด้วย และถ้าเราดึงเครื่องชั่งสปริงด้วยแรงมากเท่าใด เครื่องชั่งสปริงก็จะดึงเรากลับด้วยแรงที่มีขนาดเท่ากับแรงที่เราดึงแต่มีทิศตรงกันข้าม
จากตัวอย่างและลักษณะการเกิดแรงกระทำระหว่างวัตถุที่กล่าวไว้ด้านบน ทำให้สามารถสรุปได้ว่า เมื่อมีแรงกระทำต่อวัตถุหนึ่ง วัตถุนั้นจะออกแรงโต้ตอบในทิศตรงกันข้ามกับแรงที่มากระทำ แรงทั้งสองนี้เกิดขึ้นพร้อมกันเสมอ เราเรียกแรงที่มากระทำต่อวัตถุว่า “แรงกิริยา” (Action Force) และเรียกแรงที่วัตถุโต้ตอบต่อแรงที่มากระทำว่า “แรงปฏิกิริยา” (Reaction Force) และแรงทั้งสองนี้รวมเรียกว่า “แรงคู่กิริยา - ปฏิกิริยา” (Action – Reaction Pair)
จากการศึกษาพบว่า แรงกิริยาและแรงปฏิกิริยามีขนาดเท่ากัน แต่มีทิศทางตรงกันข้ามเสมอ นิวตันได้สรุปความสัมพันธ์ระหว่างแรงกิริยาและแรงปฏิกิริยาไว้เป็นกฎการเคลื่อนที่ข้อที่ 3 ของนิวตัน ซึ่งมีใจความว่า “ทุกแรงกิริยาจะต้องมีแรงปฏิกิริยาที่มีขนาดเท่ากันและทิศตรงข้ามกันเสมอ” ตามความสัมพันธ์ต่อไปนี้
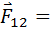 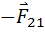
เมื่อ 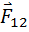 แทน แรงที่กระทำต่อวัตถุก้อนที่ 1 โดยวัตถุก้อนที่ 2 แทน แรงที่กระทำต่อวัตถุก้อนที่ 1 โดยวัตถุก้อนที่ 2
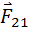 แทน แรงที่กระทำต่อวัตถุก้อนที่ 2 โดยวัตถุก้อนที่ 1 เป็นแรงปฏิกิริยาของ แทน แรงที่กระทำต่อวัตถุก้อนที่ 2 โดยวัตถุก้อนที่ 1 เป็นแรงปฏิกิริยาของ 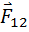
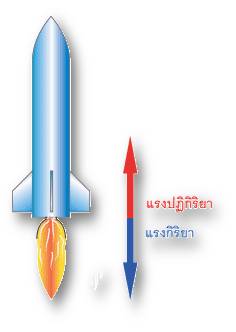
หากเราออกแรงถีบยานอวกาศในอวกาศ ทั้งตัวเราและยานอวกาศต่างเคลื่อนที่ออกจากกัน (แรงกริยา = แรงปฏิกิริยา) แต่ตัวเราจะเคลื่อนที่ด้วยความเร่งที่มากกว่ายานอวกาศ ทั้งนี้เนื่องจากตัวเรามีมวลน้อยกว่ายานอวกาศ (กฎข้อที่ 2) ดังภาพที่ 1
ภาพที่ 1 การเคลื่อนที่ในอวกาศ
นิวตันอธิบายว่า ขณะที่ดวงอาทิตย์มีแรงกระทำต่อดาวเคราะห์ ดาวเคราะห์ก็มีแรงกระทำต่อดวงอาทิตย์ในปริมาณที่เท่ากัน แต่มีทิศทางตรงกันข้าม และนั่นคือแรงดึงดูดร่วม
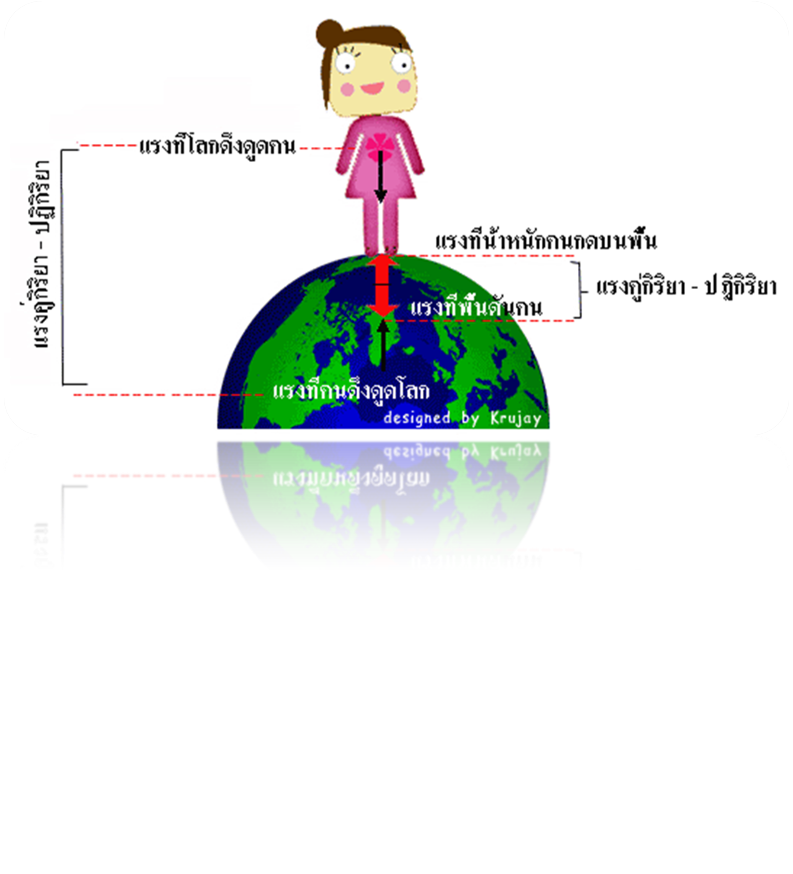
จากรูปสามารถสรุปได้ว่า
1. แรงกิริยาและแรงปฏิกิริยาจะเกิดพร้อมกันเสมอ
2. แรงคู่กิริยา – ปฏิกิริยาเป็นแรงที่กระทำต่อวัตถุคนละวัตถุกัน ดังนั้นแรงคู่นี้จึงรวมกันไม่ได้
3. แรงคู่กิริยา - ปฏิกิริยาเกิดขึ้นได้ทั้งกรณีที่วัตถุสัมผัสกันหรือไม่สัมผัสกันก็ได้
นิวตันอธิบายการเคลื่อนที่ของดาวเคราะห์ ตามกฎของเคปเลอร์
การค้นพบกฎทั้งสามข้อนี้ นำไปสู่การค้นพบ “กฎความโน้มถ่วงแห่งเอกภพ” (The Law of Universal) “วัตถุสองชิ้นดึงดูดกันด้วยแรงซึ่งแปรผันตามมวลของวัตถุ แต่แปรผกผันกับระยะทางระหว่างวัตถุยกกำลังสอง” ซึ่งเขียนเป็นสูตรได้ว่า
F = G (m1m2/ r2) โดยที่ F = แรงดึงดูดระหว่างวัตถุ
m1 = มวลของวัตถุชิ้นที่ 1
m2 = มวลของวัตถุชิ้นที่ 2
r = ระยะห่างระหว่างวัตถุทั้ง 2 ชิ้น
G = ค่าคงที่ของแรงโน้มถ่วง = 6.67×10-11 newton m2/kg2
บางครั้งเราเรียกกฎข้อนี้อย่างง่ายๆ ว่า “กฎการแปรผกผันยกกำลังสอง” (Inverse square law) นิวตันพบว่า “ขนาดของแรง จะแปรผกผันกับ ค่ากำลังสองของระยะห่างระหว่างวัตถุ”
ตัวอย่าง: เมื่อระยะทางระหว่างวัตถุเพิ่มขึ้น 2 เท่า แรงดึงดูดระหว่างวัตถุจะลดลง 4 เท่า ดังที่แสดงในภาพที่ 2 เขาอธิบายว่า การร่วงหล่นของผลแอปเปิล ก็เช่นเดียวกับการร่วงหล่นของดวงจันทร์ ณ ตำแหน่งบนพื้นผิวโลก สมมติว่าแรงโน้มถ่วงบนพื้นผิวโลกมีค่า = 1 ระยะทางจากโลกถึงดวงจันทร์มีค่า 60 เท่าของรัศมีโลก ดังนั้นแรงโน้มถ่วง ณ ตำแหน่งวงโคจรของดวงจันทร์ย่อมมีค่าลดลง = 602 = 3,600 เท่า
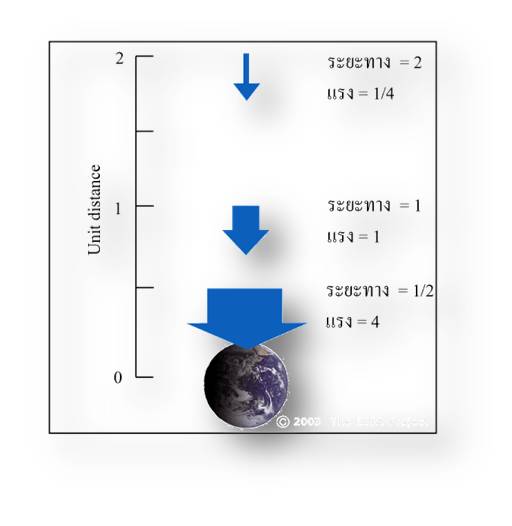
ภาพที่2 การเคลื่อนที่ในอวกาศ
ในภาพที่ 2 แสดงให้เห็นว่า ใน 1 วินาที ดวงจันทร์เคลื่อนที่ไปได้ 1 กิโลเมตร จะถูกโลกดึงดูดให้ตกลงมา 1.4 มิลลิเมตร เมื่อดวงจันทร์โคจรไปได้ 1 เดือน ทั้งแรงตั้งต้นของดวงจันทร์ และแรงโน้มถ่วงของโลก ก็จะทำให้ดวงจันทร์โคจรได้ 1 รอบพอดี เราเรียกการตกเช่นนี้ว่า “การตกแบบอิสระ” (Free fall) อันเป็นหลักการซึ่งมนุษย์นำไปประยุกต์ใช้กับการส่งยานอวกาศ และดาวเทียม ในยุคต่อมา
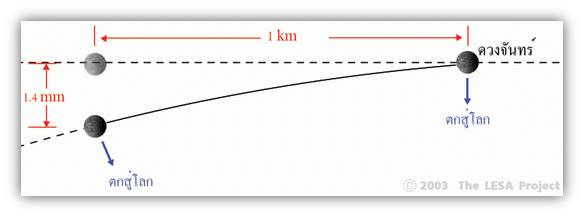
ภาพที่ 3 การเคลื่อนที่ของดวงจันทร์
ตอนที่เคปเลอร์ค้นพบกฎการเคลื่อนที่ของดาวเคราะห์ ซึ่งได้จากผลของการสังเกตการณ์ในคริสต์ศตวรรษที่ 16 นั้น เขาไม่สามารถอธิบายว่าเหตุใดจึงเป็นเช่นนั้น จวบจนอีกหนึ่งศตวรรษต่อมา นิวตันได้ใช้กฎการแปรผกผันยกกำลังสอง อธิบายเรื่องการเคลื่อนที่ของดาวเคราะห์ ตามกฎทั้งสามข้อของเคปเลอร์ ดังนี้
• ดาวเคราะห์โคจรรอบดวงอาทิตย์เป็นรูปวงรี เกี่ยวเนื่องจากระยะทางและแรงโน้มถ่วงจากดวงอาทิตย์
• ในวงโคจรรูปวงรี ดาวเคราะห์จะเคลื่อนที่เร็ว ณ ตำแหน่งใกล้ดวงอาทิตย์ และเคลื่อนที่ช้า ณ ตำแหน่งไกลจากดวงอาทิตย์ เนื่องจากอิทธิพลของระยะห่างระหว่างดวงอาทิตย์
• ดาวเคราะห์ดวงในเคลื่อนที่ได้เร็วกว่าดาวเคราะห์ดวงนอก เป็นเพราะว่าอยู่ใกล้กับดวงอาทิตย์มากกว่า จึงมีแรงโน้มถ่วงระหว่างกันมากกว่า
ความเร็ว (Speed) หมายถึง ระยะทางที่วัตถุเคลื่อนที่ไปใน 1 หน่วยของเวลา (ระยะทาง/เวลา)
ความเร่ง (Acceleration) หมายถึง ความเร็วของวัตถุที่เปลี่ยนแปลงไปใน 1 หน่วยเวลา (ระยะทาง/เวลา)/เวลา
ตัวอย่าง:
ในวินาทีแรก รถเคลื่อนที่ด้วยความเร็ว 1 เมตร/วินาที ในวินาทีที่สอง รถคันนี้เคลื่อนที่ด้วยความเร็ว 5 เมตร/วินาทีเพราะฉะนั้น รถคันนี้มีความเร่ง 4 (เมตร/วินาที)/วินาที
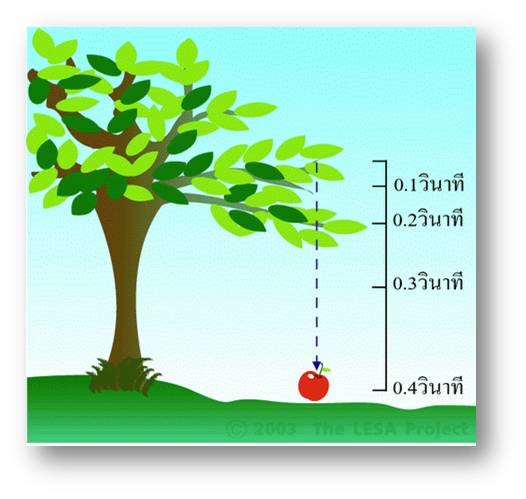
ภาพที่ 9 ความเร่งของการร่วงหล่น
ณ ตำแหน่งพื้นผิวโลก วัตถุจะร่วงหล่นสู่พื้นด้วยความเร่ง (9.8 เมตร/วินาที)/วินาที ภาพที่ 8 แสดงให้เห็นว่า ความเร็วของแอปเปิลเพิ่มมากขึ้นในแต่ละช่วงเวลา 0.1 วินาที
FAB คือ แรงที่ A กระทำบน B และ FBA คือแรงที่Bกระทำบน A
ระหว่างวัตถุทั้งสอง มีแรงอยู่ 2 แรงกระทำซึ่งกันและกันเราเรียกแรงหนึ่งว่า แรงกิริยา และอีกแรงหนึ่งเรียกว่า แรงปฏิกิริยา
ข้อสังเกต แรงคู่กิริยาและปฏิกิริยาจะต้องกระทำระหว่างวัตถุสองอัน
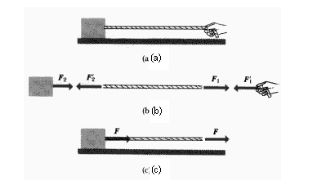
รุปที่4-10 (a) คนออกแรงดึงเชือกส่วนปลายเชือกอีกด้านหนึ่งถุกผุกติดไว้กับกล่อง
(b) แผนภาพแยกแรงเพื่อแสดงให้เห้นแรงมุมกล่อง,เส้นเชือกและแรงที่คนดึงเชือก
(c) แรงจะถูกส่งผ่านจากมือคนอื่นไปที่กล่อง
จากรุป4-10 ออกแรงดึงปลายเชือก ส่วนปลายเชือกอีกข้างหนึ่งูกติดไว้กับกล่อง
กำหนดให้ F1 คือ แรงที่ดึงเชือก F1’ แรงปฏิกิริยาที่เชือกกระทำต่อคน
F2 คือ แรงที่เชือกกระทำกับกล่อง F2’ แรงปฏิกิริยาที่กล่องกระทำกับเชือก
F1และ F2’ เป้นแรงที่มีทิศทางตรงกันข้ามที่ไม่ใช่แรงคุ่กิริยาและปฏิกิริยาเพราะว่า
แรงนี้กระทำบนวัตถุเดียวกัน ดังนั้น F1และ F2’ ไม่จำเป็นจะต้องมีขนาดเท่ากัน ในกรณีที่เชือกมีมวลและระบบกำลังเคลื่อนที่ไปทางขวาเดียวความเร่ง F1 จะมีค่ามากกว่า F2’ แรงสุทธิที่เหลือ (F1- F2’) ทำให้เชือกมีความเร่ง
อย่างไรก็ตาม ถึงระบบจะมีความเร่ง F1= F1’ และ F2= F2’ เพราะเป็นแรงกิริยาและปฏิกิริยากระทำระหว่างวัตถุ2อัน แต่ถ้าโจทย์กำหนดว่าเชือกมีมวลน้อยมาก มวลของเชือกเกือบเป็นศูนย์ F1จะเท่ากับ F2’
ขอย้ำจุดสำคัญตรงนี้อีกทีว่าแรงกิริยาและปฏิกิริยา จะไม่กระทำอยุ่บนวัตถุเดียวกัน ซึ่งจะต้องการความสับสนในการแก้ปัญหาโจทยืต่อไป
|